4 Dinámica rotacional

Tabla de Contenidos

• 4.1 Energía cinética de la rotación de un cuerpo rígido sobre un eje fijo, definición de inercia rotacional.
• 4.2 Ejemplos de inercia rotacional de sistemas de partículas.
• 4.3 Teorema de los ejes paralelos.
  
• 4.4 Inercia rotacional de los cuerpos sólidos.
• 4.5 Ejemplos de inercia rotacional de cuerpos sólidos.
  
• 4.6 Torca.
• 4.7 Ejemplos de como calcular la torca.
• 4.8 Dinámica rotacional del cuerpo rígido.
  
• 4.9 Ejemplos de la dinámica rotacional del cuerpo rígido.
• 4.10 Moviniemto de rotación y traslación combinados.
  
• 4.11 Ejemplos de moviniemto de rotación y traslación combinados.
• 4.12 Conservación del momentum angular.
• 4.13 Ejemplos de conservación del momentum angular.
  

 

4.1 Energía cinética de la rotación de un cuerpo rígido sobre un eje fijo, definición de inercia rotacional

Imaginemos un objeto girando sobre un eje fijo, con una velocidad angular $\omega$ constante. Todas las partículas que forman este objeto siguen un movimiento circular uniforme y se mueven con una rapidez$$v=\omega R,$$donde $R$ es el radio de giro. Si la energía cinética total es la suma de las energías cinéticas de todas las partículas, entonces la energía cinética total es$$E_k=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2+\mathrm{...}=\sum _{i=0}^n\frac{1}{2}{m}_i{v}_i^2\mathrm{.}$$Como sabemos que las partículas siguen todas un movimiento circular uniforme y con la misma velocidad angular $\omega$, ya que es un objeto rígido, podemos decir que la rapidez de la iésima partícula es $v_i=\omega r_i$ y por lo tanto$$E_k=\sum _{i=0}^n\frac{1}{2}{m}_i{\left(\omega R_i\right)}^2=\frac{1}{2}{\omega }^2\sum _{i=0}^n{m}_i{R}_i^2\mathrm{.}$$Para simplificar la escritura de la ecuación anterior, definamos a la cantidad $$\begin{array}{cc}I=\sum _{i=0}^n{m}_i{R}_i^2,& (1)\end{array}$$ de modo que$$E_k=\frac{1}{2}I{\omega }^2\mathrm{.}$$A la cantidad $I$ se le llama inercia rotacional (en algunos textos le llaman momento de inercia) y es el producto de la masa de cada partícula por la distancia al eje de giro elevada al cuadrado. La expresión anterior es análoga a la definición de energía cinética para una partícula $E_k=\frac{1}{2}m{v}^2$.

4.2 Ejemplos de inercia rotacional de sistemas de partículas

4.2.1 Un triángulo con partículas en sus vértices

Tres partículas de masas $m_1=2.3 kg$, $m_2=3.2 kg$ y $m_3=1.5 kg$ están en los vértices de un triángulo como el de la figura 1. (a) Halle la inercia de rotación de dicho sistema cuando el eje es perpendicular al plano de la figura y pasa por la partícula 1. (b) Ahora halle la inercia de rotación pero cuando el eje pasa por la partícula 2 y es perpendicular al plano de la figura. (c) Repita el proceso pero ahora para cuando el eje pasa por la partícula 3. (d) Halle, por último, la inercia rotacional del sistema cuando el eje de rotación es perpendicular al plano de la figura y éste pasa por el centro de masas.

Figura 1: Objeto rígido formado por tres partículas.

 

Las inercias rotacionales de los tres primeros incisos son

(a) $$I_1=m_1{\left(0\right)}^2+m_2{d}^2+m_3{l}^2=52.8 kg{m}^2\mathrm{.}$$

(b)$$I_2=m_1{d}^2+m_2{\left(0\right)}^2+m_3\left(d^2+l^2\right)=58.2 kg{m}^2\mathrm{.}$$

(c)$$I_3=m_1{l}^2+m_2\left(d^2+l^2\right)+m_3{\left(0\right)}^2=116.8 kg{m}^2\mathrm{.}$$

(d) Hay que hallar primero el centro de masa $r_{cm}$ que es una cantidad vectorial, a diferencia de la inercia rotacional $I$ que es un escalar.

Figura 2: Centro de masas del objeto de la figura 1.

 

$$x_{cm}=\frac{m_1{x}_1+m_2{x}_2+m_3{x}_3}{M}=0.857 m,$$$$y_{cm}=\frac{m_1{y}_1+m_2{y}_2+m_3{y}_3}{M}=1.37 m,$$donde $M$ representa la suma de las tres masas. Después hay que hallar la distancia al cuadrado de las tres partículas a ese centro$$r_1^2=x_{cm}^2+y_{cm}^2=2.62{ m}^2,$$$$r_2^2=x_{cm}^2+{\left[d-y_{cm}\right]}^2=3.39{ m}^2$$$$r_3^2={\left[l-x_{cm}\right]}^2+y_{cm}^2=11.76{ m}^2\mathrm{.}$$Con todo ésto ya podemos hallar la inercia rotacional respecto de un eje que pasa por el centro de masa y es perpendicular al plano $xy$$$I_{cm}=m_1{r}_1^2+m_2{r}_2^2+m_3{r}_3^2=34.51 kg{m}^2$$

4.3 Teorema de los ejes paralelos

El teorema de los ejes paralelos se puede utilizar para determinar la inercia rotacional $I$ de un cuerpo rígido, con respecto a cualquier eje, dada la inercia rotacional del cuerpo alrededor de un eje paralelo que pasa por el centro de masa del objeto $I_{cm}$ y la distancia perpendicular $h$ entre los ejes.

Figura 3: Un objeto rígido, el eje de rotación que pasa por su centro de masa y otro eje paralelo.

 

Dicho teorema dice que, dado un eje que pasa por el centro de masa de un objeto rígido y dado un segundo eje paralelo al primero, la inercia rotacional de ambos ejes está relacionada mediante la expresión: $$I=I_{cm}+m{h}^2$$donde $m$ es la masa del objeto. Su demostración es simple si expresamos la posición de cada partícula en el sistema de referencia del centro de masa.

Figura 4: Coordenadas de un punto para los diferentes sistemas de referencia.

 

La inercia rotacional escrita en términos de algún sistema de referencia arbitrario es$$I=\sum _{i=0}^n{m}_i{R}_i^2,$$donde $$R_i^2=x_i^2+y_i^2$$ pero a su vez $x_i=x{\text{'}}_i+x_{cm}$ y $y_i=y{\text{'}}_i+y_{cm}$, de modo que$$I=\sum _{i=0}^n{m}_i\left[{\left(x{\text{'}}_i+x_{cm}\right)}^2+{\left(y{\text{'}}_i+y_{cm}\right)}^2\right]\mathrm{.}$$Llevando a cabo operaciones queda$$I=\sum _{i=0}^n{m}_i\left[\left(x_i^{\prime 2}+x_{cm}^2+2x{\text{'}}_i{x}_{cm}\right)+\left(y^{\prime 2}+y_{cm}^2+2y{\text{'}}_i{y}_{cm}\right)\right]$$y reagrupando los términos$$I=\sum _{i=0}^n{m}_i\left(x_i^{\prime 2}+y{}_i^{\prime 2}\right)+2x_{cm}\sum _{i=0}^n{m}_{i}x{\text{'}}_i+2y_{cm}\sum _{i=0}^n{m}_{i}y{\text{'}}_i+\left(x_{cm}^2+y_{cm}^2\right)\sum _{i=0}^n{m}_i\mathrm{.}$$La primera sumatoria no es más que la inercia rotacional respecto de un eje que pasa por el centro de masas, es decir $I_{cm}$. La segunda es proporcional a la coordenada $x$ del centro de masa, pero en el sistema de referencia en el que dicho centro de masa está en el origen, es decir se anula. Lo mismo pasa con la tercera sumatoria, pero la última es el producto de $h$ por la masa del objeto, así que finalmente se demuestra el teorema de los ejes paralelos.

4.4 Inercia rotacional de los cuerpos sólidos

La definición de inercia rotacional para sistemas de partículas se puede generalizar a objetos sólidos tomando el límite cuando los elementos de masa son infinitamente pequeños

$$I=\underset{\delta m_i\to 0}{lim}\sum R_i^2\delta m_i$$de modo que la sumatoria se transforma en una integral$$I=\int R^{2}dm\mathrm{.}$$

4.5 Ejemplos de inercia rotacional de cuerpos sólidos

4.5.1 La varilla delgada que gira en torno a un eje que pasa por su centro de masa

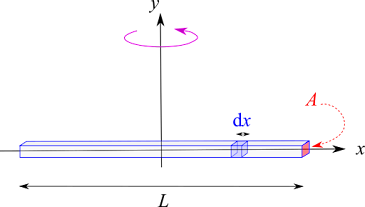
Encuentre la inercia de rotación de una varilla delgada y de densidad uniforme, de longitud $L$y masa $M$, que gira en torno a un eje que pasa por su centro de masa y es perpendicular a ésta.

Figura 5: Varilla delgada que rota en torno a un eje que pasa por su centro y es perpendicular a ésta. Se muestra una diferencial de masa, que tiene un ancho $dx$.

 

La diferencial de masa es una rebanada muy delgada de la varilla: $dm=\rho Adx$, donde $\rho$ es la densidad, $A$ es el área de la sección y $dx$ la diferencial de longitud. La integral queda$$I_{cm}=\int r^{2}dm=\rho A{\int }_{-L/2}^{L/2}{x}^{2}dx=\rho A\frac{1}{3}{.x^3|}_{-L/2}^{L/2}=\rho A\frac{2}{3}{\left(\frac{L}{2}\right)}^3=\rho A\frac{L^3}{12},$$Pero como la densidad es la masa entre el volumen $\rho =\frac{M}{AL}$ lo anterior se transforma en$$I_{cm}=\frac{1}{12}M{L}^2\mathrm{.}$$

4.5.2 La varilla delgada en torno a un eje que pasa por su extremo

Encuentre la inercia de rotación de una varilla delgada y de densidad uniforme, de longitud $L$y masa $M$, que gira en torno a un eje que pasa por su extremo y es perpendicular a ella.

Figura 6: Varilla delgada que rota en torno a un eje que pasa por uno de sus extremos y es perpendicular a ésta.

 

Empleando el teorema de los ejes paralelos$$I=I_{cm}+m{h}^2=\frac{1}{12}M{L}^2+M{\left(\frac{1}{2}L\right)}^2=\frac{1}{3}M{L}^2\mathrm{.}$$

4.5.3 La placa rectangular delgada en torno a un eje que pasa por su centro de masa

Encuentre la inercia rotacional de una placa rectangular, de densidad uniforme, cuando gira en torno a un eje que pasa por su centro de masa y es perpendicular a ella. Sea la masa de la placa $M$, sus dimensiones en largo y ancho $l$ y $a$.

Figura 7: Placa rectangular, de densidad uniforme, que gira en torno a un eje que pasa por su centro de masa.

 

Se puede pensar que una placa está formada por una infinidad de varillas delgadas, de masa $dm$, que están a una distancia $x$ del centro de masa. Una diferencial de la inercia rotacional de la placa, que corresponde a una de las varillas de las mencionadas es$$dI=\frac{1}{12}{l}^{2}dm+x^{2}dm\mathrm{.}$$Aquí la diferencial de masa es$$dm=\sigma ldx$$donde $\sigma$ es la densidad superficial de masa, substituyendo esta diferencial de masa en la ecuación para $dI$ queda$$dI=\frac{1}{12}{l}^3\sigma dx+x^2\sigma ldx\mathrm{.}$$Esta expresión se puede integrar en la variable $x$ desde $-a/2$ hasta $a/2$$$I=\frac{1}{12}{l}^3\sigma a+\frac{2}{3}{\left(\frac{a}{2}\right)}^3\sigma l=\frac{\sigma }{12}a{l}^3+\frac{\sigma }{12}{a}^{3}l,$$pero la densidad superficial de masa es simplemente la masa entre el área $\sigma =\frac{M}{al},$ entonces$$I=\frac{M}{12}\left(l^2+a^2\right)\mathrm{.}$$

4.6 Torca

Por experiencia sabemos que si queremos hacer rotar una puerta partiendo del reposo, es más eficiente aplicar la fuerza lo más lejos del eje de giro que se pueda y lo más perpendicular a la puerta posible.

 

 

Figura 8: Puerta a la que se le aplican distintas fuerzas con el objetivo de que comience a rotar.

 

Una fuerza grande pero muy cerca del eje de giro, como $F_a$ de la figura 8, no hará fácil el trabajo. Aplicar la fuerza paralela al plano de la puerta, $F_b$, tampoco será eficiente. Si en cambio, se aplica la fuerza lejos del eje de giro y de manera perpendicular a la superficie de la puerta, $F_c$ , será lo mejor. Sea el vector $R$ el que parte desde el eje de giro hasta el punto de aplicación de la fuerza, como indica la figura 9, entre mayor sea la magnitud del producto vectorial $R\times F$, más fácilmente podremos empezar a rotar la puerta, esa magnitud será igual a $RFsin\theta$. A este producto lo podemos nombrar “torca” y representarla con el símbolo $\stackrel{⟶}{\tau }$ $$\begin{array}{cc}\stackrel{⟶}{\tau }=R\times F& (2)\end{array}$$y su magnitud es$$\tau =RFsin\theta \mathrm{.}$$Un esquema se muestra en la figura 9.

 Figura 9: Puerta, vista desde arriba, a la que se le aplica una fuerza $F$.

 

 La torca descrita por (2) es una cantidad vectorial, si hay varias fuerzas actuando sobre el objeto que se quiere hacer rotar, las torcas correspondientes se suman como vectores. La dirección de la torca es perpendicular al plano de giro. Mirando desde arriba al objeto que gira, si se tiende a hacer girar el objeto en el sentido antihorario, la torca apunta hacia arriba (hacia nosotros) y si se tiende a hacer girar al objeto en sentido horario, la torca apunta hacia abajo. En el caso de la fuerza que se muestra en la figura 9, la torca apunta hacia adentro de la página.

4.7 Ejemplos de como calcular la torca

4.7.1 Dos fuerzas que ejercen torca

La figura 10 muestra los radios de giro y los puntos de aplicación de dos fuerzas en torno al origen. Imagine que estas fuerzas actúan sobre un cuerpo rígido pivoteado en el origen, estando todos los vectores en el plano de la figura. (a) Halle una expresión simbólica para la magnitud de la torca resultante sobre el cuerpo. (b) Si $R_1=1.30 m$, $R_2=2.15 m$, $F_1=4.20 N$, $F_2=4.90 N$, ${\theta }_1=75°$ y ${\theta }_2=58°$ , ¿cuáles son la magnitud y la dirección de la torca resultante? 

 Figura 10: Los radios de giro y los puntos de aplicación de dos fuerzas en torno al origen $O$.

 

(a) La primera torca ${\stackrel{⟶}{\tau }}_1$ es $${\stackrel{⟶}{\tau }}_1=R_1\times F_1=R_1{F}_{1}sin{\theta }_1\hat{\odot },$$donde $\hat{\odot }$ representa un vector unitario que sale de la página. La segunda torca es$${\stackrel{⟶}{\tau }}_2=R_2\times F_2=R_2{F}_{2}sin{\theta }_2\hat{\otimes },$$donde $\hat{\otimes }$ representa un vector unitario que entra a la página. La suma de las dos torcas es$${\stackrel{⟶}{\tau }}_1+{\stackrel{⟶}{\tau }}_2=R_1{F}_{1}sin{\theta }_1\hat{\odot }+R_2{F}_{2}sin{\theta }_2\hat{\otimes }\mathrm{.}$$

(b) Ya con los datos numéricos se puede llegar al resultado (sin olvidar que las dos torcas apuntan en sentido contrario)$${\stackrel{⟶}{\tau }}_1+{\stackrel{⟶}{\tau }}_2=\left(1.30 m\right)\left(4.20 N\right)sin\left(75°\right)\hat{\odot }+\left(2.15 m\right)\left(4.90 N\right)sin\left(58°\right)\hat{\otimes }=\left(3.66 Nm\right)\hat{\otimes },$$la torca resultante entra a la página.

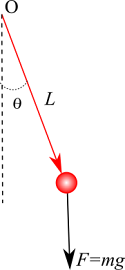
4.7.2 Torca en el péndulo simple

Un péndulo consta de un cuerpo de masa $m=0.17 kg$ en el extremo de una varilla rígida de longitud $L=1.25 m$ y masa despreciable. (a) ¿Cuál es la magnitud de la torca debida a la gravedad en torno al punto O, que está fijo, en el instante en que el péndulo se ha desplazado un ángulo $\mathrm{\theta \; =\; 11°}$ respecto de la vertical? (b) ¿Cuál es la dirección de la torca en ese instante? (c) ¿Depende la dirección de la torca de que el péndulo esté a la izquierda o a la derecha de la posición vertical?

 Figura 11: Péndulo simple y una animación del mismo. Se puede acceder a la animación original en https://upload.wikimedia.org/wikipedia/commons/8/82/Simple_Pendulum.gif.

 

El diagrama de cuerpo libre se muestra en la figura 11, se encuentran actuando sobre el cuerpo tanto la tensión como la gravedad, pero la tensión no ejerce torca ya que es paralela al eje de giro. (a) La torca correspondiente es $$\stackrel{⟶}{\tau }=L\times mg=Lmgsin\theta \hat{\otimes },$$su magnitud es $Lmgsin\theta =0.397 Nm$. (b) La dirección de la torca entra a la página. (c) La dirección de la torca depende de la posición del péndulo, si está a la izquierda de la vertical (línea punteada en la figura 11) la torca sale de la página.

4.7.3 Torca en el péndulo físico

Si el péndulo consiste ahora sólo de una varilla delgada de masa $m$ y la varilla se pivotea en su extremo (a) ¿Cuál es la magnitud de la torca debida a la gravedad en torno al pivote, en el instante en que el péndulo se ha desplazado un ángulo $\theta$ respecto de la vertical? (b) Si ahora el eje de giro se atraviesa por el centro de masas ¿cuál sería la torca sobre la varilla?

Figura 12: Péndulo físico hecho con una varilla delgada, con el eje de giro pasando por un extremo.

 

(a) Se puede pensar que la varilla está conformada por una gran cantidad de rebanadas infinitesimales. El peso de cada diferencial de masa ejerce torca sobre la varilla, aunque todas estas torcas infinitesimales tienen la misma dirección (entra a la página), cada diferencial tiene un radio de giro $x$ distinto. Si se suman las torcas de todas las diferenciales con una integral su magnitud resulta ser $$\tau =gsin\theta \int xdm,$$pero aquí la integral $\int xdm$ está relacionada con el centro de masa$$\int xdm=m{x}_{cm}$$por lo que$$\tau =mg{x}_{cm}sin\theta =mg\frac{L}{2}sin\theta \mathrm{.}$$

(b) Si el pivote pasa por el centro de masa, la mitad de la varilla de arriba ejerce una torca cuya dirección sale de la página y tiende a hacer girar la varilla en sentido antihorario, mientras que la mitad de abajo ejerce torca en sentido contrario. Como las dos mitades de varilla son iguales y hacen el mismo ángulo con la vertical, las dos torcas son iguales en magnitud, pero siendo sus direcciones contrarias éstas se anulan. Al sostener la varilla por su centro de masa, la gravedad no ejerce torca neta.

4.8 Dinámica rotacional del cuerpo rígido

Si comenzamos con la segunda ley de Newton para una partícula, la iésima partícula de un sistema, $$F_i=m_i{a}_i,$$donde $F_i$ es la fuerza neta sobre esa partícula, y luego multiplicamos vectorialmente todo por $R_i$ del lado izquierdo, queda $$R_i\times F_i=R_i\times m_i{a}_i,$$del lado izquierdo se tiene la torca neta para la iésima partícula y del derecho la masa por el producto $R_i\times a_i$$${\stackrel{⟶}{\tau }}_i=m_i\left(R_i\times a_i\right)\mathrm{.}$$Debido a que $a=\frac{dv}{dt}$ también se puede escribir$${\stackrel{⟶}{\tau }}_i=m_i\left(R_i\times \frac{d{v}_i}{dt}\right),$$aquí es conveniente recordar que si se trata de un movimiento circular se cumplen las siguientes relaciones$$v_i=\stackrel{⟶}{\omega }\times R_i y \frac{d{R}_i}{dt}=v_i,$$donde $\stackrel{⟶}{\omega }$ es la misma para todas las partículas del sistema si se trata de un cuerpo rígido. Así que podemos obtener$${\stackrel{⟶}{\tau }}_i=m_i\left(R_i\times \frac{d\left(\stackrel{⟶}{\omega }\times R_i\right)}{dt}\right)=m_i\left[R_i\times \left(\frac{d\stackrel{⟶}{\omega }}{dt}\times R_i+\stackrel{⟶}{\omega }\times \frac{d{R}_i}{dt}\right)\right]$$y si además recordamos que $\frac{d\stackrel{⟶}{\omega }}{dt}=\stackrel{⟶}{\alpha }$, queda$${\stackrel{⟶}{\tau }}_i=m\left[R_i\times \left(\stackrel{⟶}{\alpha }\times R_i+\stackrel{⟶}{\omega }\times v_i\right)\right]\mathrm{.}$$En la expresión anterior tenemos implicados dos triples productos $R_i\times \left(\stackrel{⟶}{\alpha }\times R_i\right)$ y $R_i\times \left(\stackrel{⟶}{\omega }\times v_i\right)$ que si empleamos la identidad del álgebra vectorial $A\times \left(B\times C\right)=B\left(A\cdot C\right)-C\left(A\cdot B\right)$ se pueden reescribir en términos de productos escalares$$R_i\times \left(\stackrel{⟶}{\alpha }\times R_i\right)=\stackrel{⟶}{\alpha }\left(R_i\cdot R_i\right)-R_i\left(R_i\cdot \stackrel{⟶}{\alpha }\right)$$y$$R_i\times \left(\stackrel{⟶}{\omega }\times v_i\right)=\stackrel{⟶}{\omega }\left(R_i\cdot v_i\right)-v_i\left(R_i\cdot \stackrel{⟶}{\omega }\right),$$resultados que se pueden interpretar.

En el movimiento circular uniforme, la velocidad $v$, el radio de giro $R$ y la velocidad angular $\stackrel{⟶}{\omega }$ son vectores perpendiculares entre sí. Sucede lo mismo cuando se trata de movimiento circular con aceleración angular constante, además en este caso la aceleración angular vectorial $\stackrel{⟶}{\alpha }$ es paralela a $\stackrel{⟶}{\omega }$. Por lo anterior los productos escalares $R_i\cdot \stackrel{⟶}{\alpha }$, $R_i\cdot v$ y $R_i\cdot \stackrel{⟶}{\omega }$ se anulan y expresión para la torca neta sobre la partícula se reduce a$${\stackrel{⟶}{\tau }}_i=m_i\stackrel{⟶}{\alpha }\left(R_i\cdot R_i\right)=m_i{R}_i^2\stackrel{⟶}{\alpha },$$aquí la cantidad $m_i{R}_i^2$ no es otra cosa que la inercia rotacional de la partícula. Si ahora sumamos sobre todas las partículas que conforman un sistema $$\sum _{i=1}^n{\stackrel{⟶}{\tau }}_i=\sum _{i=1}^n{m}_i{R}_i^2\stackrel{⟶}{\alpha },$$dado que tenemos un objeto rígido $\stackrel{⟶}{\alpha }$ es la misma para todas las partículas y por lo tanto podemos resumir lo anterior a$${\stackrel{⟶}{\tau }}_{neta}=I\stackrel{⟶}{\alpha },$$que es una versión de la segunda ley de Newton para las rotaciones.

4.9 Ejemplos de la dinámica rotacional del cuerpo rígido

4.9.1 Disco y pesa

La figura 13 muestra un disco uniforme de masa $M=2.5 kg$ y radio $R=20 cm$ montado en un eje horizontal fijo y sin fricción. La inercia rotacional de un disco de densidad uniforme que gira en torno a su centro, siendo el eje de rotación perpendicular a su superficie es $\frac{1}{2}M{R}^2$. Un bloque de masa $m=1.2 kg$ cuelga de una cuerda ideal que pasa alrededor del borde del disco. Halle la magnitud de la aceleración $a$ del bloque al caer, la de la tensión $T$ en el cordón y la aceleración angular $\alpha$ del disco. 

 Figura 13: Disco y pesa.

 

El objeto que cuelga tiene un movimiento de traslación y su aceleración depende de las fuerzas que actúan sobre éste. El disco sin embargo, no se traslada, sólo rota sobre su eje que está en su centro geométrico, la aceleración angular que presente será resultado de las torcas que actúen sobre él. Un diagrama de cuerpo libre para ambos objetos se muestra en la figura 14.

 Figura 14: Diagrama de cuerpo libre de los objetos de la figura 13.

 

Para el bloque, la segunda ley de Newton se resume en una ecuación $$\begin{array}{cc}T-mg=-ma\mathrm{.}& (3)\end{array}$$El eje del disco está fijo, el disco no se acelera ni se mueve de manera traslacional, las tres fuerzas que actúan sobre éste deben estar en equilibrio$$F_{techo}-T-Mg=0.$$El movimiento relevante del disco es el rotacional, la suma de las torcas que actúan sobre éste determinan su aceleración angular. Dado que el disco está sostenido por su centro de masa, la gravedad no ejerce torca sobre él, sin embargo, la tensión de la cuerda sí $$\begin{array}{cc}TRsin\theta =I\alpha ,& (4)\end{array}$$donde $\theta =90°$. Las ecuaciones 3 y 4 forman un sistema de dos ecuaciones con tres incógnitas $a$, $T$, y $\alpha$, pero aún hay una pieza de información que no hemos empleado. Se puede suponer que la cuerda no desliza sobre la superficie del disco, de modo que el la rapidez traslacional del bloque coincide con la velocidad tangencial del borde del disco. Así mismo la aceleración del bloque debe coincidir con la aceleración del borde del disco $$\begin{array}{cc}a=\alpha R\mathrm{.}& (5)\end{array}$$Las ecuaciones 3, 4 y 5 forman un sistema de tres ecuaciones y tres incógnitas que podemos resolver. Substituyendo 5 en 4 se obtiene$$TRsin\theta =I\frac{a}{R}$$y luego despejando la tensión y sustituyéndola en 3 queda$$\frac{Ia}{R^{2}sin\theta }-mg=-ma\mathrm{.}$$Despejando la aceleración se obtiene$$a=\frac{g}{\frac{I}{m{R}^{2}sin\theta }+1}=\frac{g}{\frac{M}{2m}+1}=4.8 m/s^2\mathrm{.}$$Ahora se puede calcular muy fácilmente la tensión con 3$$T=m\left(g-a\right)=6.0 N$$y la aceleración angular $\alpha$ con 5$$\alpha =\frac{a}{R}=24 rad/s^2\mathrm{.}$$

0.0.1 Máquina de Atwood con inercia rotacional

Considere dos pesas que tienen diferentes masas $m_1$ y $m_2$, atadas a una cuerda que pasa sobre una polea, como se muestra en la figura 15. La polea tiene un radio $R$ y momento de inercia $I$ respecto de su eje de rotación. La cuerda no se desliza sobre polea y el sistema se suelta desde el reposo. (a) Encuentra la magnitud de la aceleración de los cilindros y la aceleración angular de la polea (en términos de $m_1$, $m_2$, $g$, $R$ y $I$). (b) Encuentra las magnitudes de las dos tensiones implicadas.  

Figura 15: a) Máquina de Atwood, la polea tiene masa e inercia rotacional. b) Diagrama de cuerpo libre de las pesas y la polea, en este último caso sólo se muestran las fuerzas que ejercen torca.

(a) El diagrama de cuerpo libre para los tres objetos se muestra en la figura 15 b). Como la polea no sufre movimiento de traslación sólo se muestran las fuerzas que ejercen torca. Las ecuaciones que representan a la segunda ley de Newton traslacional para las dos pesas y la que representa la dinámica rotacional de la polea son$$T_1-m_{1}g=m_{1}a,$$$$T_2-m_{2}g=-m_{2}a,$$$$R\left(T_2-T_1\right)=I\alpha \mathrm{.}$$Además, la condición de no deslizamiento es $$a=\alpha R\mathrm{.}$$Combinando estas cuatro ecuaciones se obtiene$$m_2\left(g-a\right)-m_1\left(g+a\right)=I\frac{a}{R^2},$$de donde se puede despejar a la magnitud de la aceleración$$a=\frac{g\left(m_2-m_1\right)}{\frac{I}{R^2}+m_1+m_2}\mathrm{.}$$La aceleración angular es simplemente $\frac{a}{R}$$$a=\frac{g\left(m_2-m_1\right)}{\frac{I}{R}+R\left(m_1+m_2\right)}\mathrm{.}$$(b) La tensiones son$$T_1=m_1\left(g+a\right),$$$$T_2=m_2\left(g-a\right),$$por lo que $$T_1=g\left(m_1+\frac{m_1\left(m_2-m_1\right)}{\frac{I}{R}+R\left(m_1+m_2\right)}\right)$$y$$T_2=g\left(m_2-\frac{m_2\left(m_2-m_1\right)}{\frac{I}{R}+R\left(m_1+m_2\right)}\right)\mathrm{.}$$

$$\mathrm{<br>}$$

4.10 Movimiento de rotación y traslación combinados

Si un objeto rota alrededor de un eje que pasa por su centro de masas y además este objeto se traslada, manteniendo el eje de giro su dirección original, podemos aplicar lo visto aquí para describir su movimiento. Lo primero que se puede demostrar en este caso es que la energía cinética total puede separarse claramente en dos partes: la traslacional y la rotacional. La energía cinética de un sistema de partículas no es otra cosa que la suma de las energías cinéticas de todas sus partículas$$E_k=\sum _i\frac{1}{2}{m}_i{v}_i^2\mathrm{.}$$Pero recordemos que la velocidad de una partícula se puede escribir como la suma de la velocidad de ésta respecto al sistema de referencia anclado al centro de masa del sistema, más la velocidad del centro de masas respecto a otro observador inercial (movimiento relativo)$$v_i=v_i^{\prime }+v_{cm},$$donde $v_i^{\prime }$ es la velocidad de la partícula respecto del centro de masas del sistema. Elevando al cuadrado esta velocidad queda$$v_i\cdot v_i=v_i^{\prime }\cdot v_i^{\prime }+2v_i^{\prime }\cdot v_{cm}+v_i\cdot v_i=v_i^{\prime 2}+2v_i^{\prime }\cdot v_{cm}+v_{cm}^2\mathrm{.}$$Introduciendo lo anterior en la sumatoria se obtiene$$E_k=\frac{1}{2}\sum _i{m}_i{v}_i^{\prime 2}+v_{cm}\cdot \sum _i{m}_i{v}_i^{\prime }+\frac{1}{2}{v}_{cm}^2\sum _i{m}_i,$$El primer grupo de términos $\frac{1}{2}\sum _i{m}_i{v}_i^{\prime 2}$ representa la energía cinética de rotación, pues en el sistema de referencia del centro de masas, el objeto sólo rota. El tercer grupo es la energía cinética de traslación de todo el objeto $\frac{1}{2}{v}_{cm}^2\sum _i{m}_i=\frac{1}{2}M{v}_{cm}^2$. El grupo de en medio tiene como factor el momentum lineal del objeto respecto al sistema de referencia del centro de masa $\sum _i{m}_i{v}_i^{\prime }$, que se anula pues ese sistema de referencia en el que el centro de masa está fijo, por definición. La energía cinética total es pues separable en una parte rotacional y la otra traslacional$$E_k=\frac{1}{2}{\omega }^2\sum _i{m}_i{r}_i^{\prime 2}+\frac{1}{2}M{v}_{cm}^2,$$donde se ha substituido $v_i^{\prime 2}={\omega }^2{r}_i^2$. Después de un segundo vistazo a este resultado, si notamos que $\sum _i{m}_i{r}_i^{\prime 2}$ no es más que la inercia rotacional del sistema de partículas, se puede simplificar la expresión aún más$$E_k=\frac{1}{2}I{\omega }^2+\frac{1}{2}M{v}_{cm}^2\mathrm{.}$$

Para describir la dinámica de la parte traslacional del movimiento podemos emplear la segunda ley de Newton $\sum F=Ma$ y para describir la parte rotacional $\sum \stackrel{⟶}{\tau }=I\stackrel{⟶}{\alpha }\mathrm{.}$

4.10.1 Condición de no deslizamiento

Si el movimiento de traslación y rotación combinados es tal que un objeto va rodando sin que haya deslizamiento relativo entre las superficies del piso y el objeto, la velocidad tangencial de rotación se relaciona con la velocidad de traslación de la siguiente manera$$v_{cm}=\omega R,$$donde $R$ es el radio de giro exterior (o de la porción del objeto que entra en contacto con la superficie sobre la que rueda). Así mismo se debe cumplir$$a_{cm}=\alpha R\mathrm{.}$$  A las trayectorias que siguen los distintos elemntos de masa de un objeto que rota y se traslada así se les llama cicloides.

 

Figura 16: Arriba: Objeto rodando sin deslizarse, el eje de rotación pasa por su centro de masa. Las flechas rojas indican la velocidad de los puntos indicados de la rueda. Abajo: animación del movimiento y el trazo de una cicloide. La animación original se puede ver en https://upload.wikimedia.org/wikipedia/commons/f/f0/Cycloid_animated_.gif.

4.11 Ejemplos de movimiento de rotación y traslación combinados

4.11.1 Rueda cilíndrica

Se comienza a rodar un disco, de densidad uniforme, sobre una superficie horizontal, con fricción, empleando una fuerza $F$ horizontal como se muestra en la figura 17. La masa del disco es $M$, su radio exterior es $R$, la inercia rotacional del disco rotando respecto de un eje que pasa por su centro de masa es $I=\frac{1}{2}M{R}^2$. (a) ¿Cuál es la magnitud de su aceleración? (b) Halle es la magnitud de la fuerza de fricción.

 

Figura 17: Un disco cilíndrico que se hace rodar.

Se muestra el diagrama de cuerpo libre del objeto en la figura 18. Se deben cumplir las siguientes condiciones, para el movimiento translacional $\sum F=ma$, por componentes horizontal y vertical$$F+f_s=M{a}_{cm},$$y$$N-Mg=0,$$para el movimiento rotacional $\sum \stackrel{⟶}{\tau }=I\stackrel{⟶}{\alpha }$$$R{f}_s-RF=-I\alpha \mathrm{.}$$Si rueda sin resbalar también se cumple$$a_{cm}=\alpha R\mathrm{.}$$$$\mathrm{ <div\; class="separator"\; style="clear:\; both;\; text-align:\; center;"><a\; href="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjENSeT1bQsdbvvsMFhK3QvYvJtLQRcpHLOoJJSATlYCoBv-N3v\_B47EvC3fyExALr1o833x5KEX5nGGITmFybmEWeCOsFouP-9-XpGx9egQAFx5eJOoYfSRqHbuw5owNqSWAkax5Q8qgqvFw8SVpvLd5GstZ7cEZmgcT9J0WXX4mtvRbPkvsYgBAvQ3\_Jg/s454/RuedaCilindrica01.png"\; style="margin-left:\; 1em;\; margin-right:\; 1em;"><img\; border="0"\; data-original-height="454"\; data-original-width="291"\; height="270"\; src="https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjENSeT1bQsdbvvsMFhK3QvYvJtLQRcpHLOoJJSATlYCoBv-N3v\_B47EvC3fyExALr1o833x5KEX5nGGITmFybmEWeCOsFouP-9-XpGx9egQAFx5eJOoYfSRqHbuw5owNqSWAkax5Q8qgqvFw8SVpvLd5GstZ7cEZmgcT9J0WXX4mtvRbPkvsYgBAvQ3\_Jg/w173-h270/RuedaCilindrica01.png"\; width="173"></a></div><br>}$$Figura 18: Diagrama de cuerpo libre correspondiente al aobjeto de la figura 17.

Las cuatro ecuaciones anteriores forman un sistema con cuatro incógnitas ($a$, $f_s$, $\alpha$ y $N$), que se puede resolver. (a) Primero se puede reescribir la ecuación de las torcas en términos de la aceleración del centro de masas$$f_s-F=-I\frac{a}{R^2}$$y luego combinando esta expresión con la ecuación de las fuerzas queda$$2F=a\left(M+\frac{I}{R^2}\right),$$de donde se puede despejar a la aceleración$$a=\left(\frac{2}{M+\frac{I}{R^2}}\right)F\mathrm{.}$$Empleando la expresión para la inercia rotacional del disco queda$$a=\frac{1}{M}\left(\frac{2}{1+\frac{1}{2}}\right)F=\left(\frac{4}{3}\right)\frac{F}{M}\mathrm{.}$$(b) Substituyendo lo anterior en la ecuación de las fuerzas, $f_s=Ma-F$, queda$$f_s=\left(\frac{4}{3}\right)F-F=\frac{1}{3}F$$

4.11.2 Rueda cilíndrica en el plano inclinado

Se tiene un disco cilíndrico que rueda sin deslizarse sobre un plano inclinado, la inclinación del plano respecto de la horizontal es $\theta$. Note que debe haber fricción estática entre el disco y el plano para que pueda rodar. (a) Halle la aceleración del centro de masa, (b) ¿es ésta mayor o menor que si simplemente resbalara sin fricción?

 

 Figura 19: Disco cilíndrico que rueda sin deslizarse sobre un plano inclinado

El diagrama de cuerpo libre se muestra en la figura 19, con el sistema de referencia propuesto. Las ecuaciones que se deben cumplir para los movimientos traslacional y rotacional son$$mgsin\theta -f_s=m{a}_{cm},$$$$N-mgcos\theta =0,$$$$-R{f}_s=-I\alpha$$y$$a_{cm}=\alpha R\mathrm{.}$$(a) Combinando las cuatro ecuaciones anteriores, llevando a cabo algunos pasos de álgebra permiten encontrar la aceleración del centro de masa$$a_{cm}=\frac{2}{3}gsin\theta ,$$que no depende de la masa del objeto. (b) La aceleración encontrada es menor a la que llevaría el objeto si se deslizara sin fricción.

Este ejercicio tembién se puede resolver con argumentos de energía, pues la energía se conserva dado que la fricción es estática, es decir que no hay deslizamiento. Si el objeto que rueda parte desde el reposo, inicialmente tiene una energía mecánica que es igual a su potencial inicial $$U_0=mgh,$$donde $h$ es la altura descendida, es decir $h=dsin\theta$, siendo $d$ la distancia recorrida. La energía al acabar el descenso es cinética y a ello contribuyen la traslación y la rotación $$E_{kf}=\frac{1}{2}m{v}_{cmf}^2+\frac{1}{2}I{\omega }_f^2,$$empleando la condición de no deslizamiento se puede reescribir$$E_{kf}=\frac{1}{2}m{v}_{cmf}^2+\frac{1}{2}I\frac{v_{cmf}^2}{R^2},$$y se puede simplificar aún más con la forma explícita para la inercia rotacional$$E_{kf}=\frac{3}{4}m{v}_{cmf}^2\mathrm{.}$$Si la energía se ha de conservar se debe cumplir $U_0=E_{kf}$, es decir$$gdsin\theta =\frac{3}{4}{v}_{cmf}^2\mathrm{.}$$Si recordamos la ecuación que relaciona la rapidez con el desplazamiento para un movimiento uniformemente acelerado, $v_f^2=v_0^2+2ad$, dado que la velocidad inicial se anula$$v_{cmf}^2=2a_{cm}d\mathrm{.}$$Combinando la expresión anterior con la de la conservación de la energía se obtiene el resultado esperado$$\frac{2}{3}gsin\theta =a_{cm}\mathrm{.}$$

Es sorprendente que la fricción actúa frenando un poco al objeto en su descenso y sin embargo, la fuerza de fricción no hace trabajo, porque no se pierde energía mecánica.

Si el objeto que rueda cuesta abajo no es un disco, sino algún otro objeto que pueda rodar de la misma manera y que su inercia rotacional se pueda escribir como $I=qM{R}^2$, donde $q$ es alguna fracción se puede concluir de manera más general que$$a_{cm}=\left(\frac{1}{1+q}\right)gsin\theta ,$$de modo que, entre mayor sea el valor de $q$, menor será la magnitud de la aceleración del centro de masa.

4.12 Conservación del momentum angular

Hasta ahora hemos descrito movimientos de rotación en torno a ejes de los que conocemos su posición y que mantienen su dirección en el tiempo, en general no siempre es así. Un buen ejemplo de ésto es el movimiento del trompo, el eje principal de rotación del trompo a su vez gira llevando a cabo un movimiento llamado de precesión.

Figura 20: Se puede acceder a la animación del movimiento del trompo original en https://giphy.com/gifs/movie-leo-inception-9UqRcQHzBou6A .

 Sin embargo, también se puede decir algo relevante y simple sobre el movimiento de rotación, aunque no se trate de un objeto rígdo o que el eje de rotación cambie su dirección. Retomando la Segunda ley de Newton para la partícula $F_i=m_i{a}_i,$ y multiplicándola por el vector de posición del lado izquierdo se obtiene$$r_i\times F_i=m_i{r}_i\times a_i\mathrm{.}$$El producto $r\times F$ es la definición más general de torca $\stackrel{⟶}{\tau }$, así que se puede escribir$${\stackrel{⟶}{\tau }}_i=m_i{r}_i\times a_i,$$pero la aceleración no es más que la derivada de la velocidad en el tiempo$${\stackrel{⟶}{\tau }}_i=m_i{r}_i\times \frac{d{v}_i}{dt}\mathrm{.}$$Empleando la identidad del cálculo vectorial $\frac{d}{dx}\left(A\times B\right)=\left(\frac{dA}{dx}\times B\right)+\left(A\times \frac{dB}{dx}\right)$ lo anterior se puede reescribir$${\stackrel{⟶}{\tau }}_i=m_i\left[\frac{d}{dt}\left(r_i\times v_i\right)-\left(\frac{d{r}_i}{dx}\times v_i\right)\right],$$pero $\frac{d{r}_i}{dx}=v_i$, de modo que el producto $$\frac{d{r}_i}{dx}\times v_i=v_i\times v_i$$ se anula, pues el resultado de todo vector “cruz-multiplicado” por sí mismo es cero. Finalmente podemos decir que$${\stackrel{⟶}{\tau }}_i=\frac{d}{dt}\left(r_i\times m_i{v}_i\right),$$este resultado es importante, pues implica que si no hay una torca neta sobre la partícula, se conserva la cantidad $r_i\times m_i{v}_i$. Este hecho es muy similar al que hemos visto en la primera unidad: si no hay fuerza neta se conserva el momentum lineal, por lo mismo a la cantidad mencionada se le llama momentum angular y se le representa con el símbolo $l$$$l=r\times mv=r\times p\mathrm{.}$$Si llevamos a cabo la suma de todas las torcas sobre un sistema de partículas podemos decir$$\sum _i{\stackrel{⟶}{\tau }}_i=\frac{d}{dt}\sum _i{l}_i$$ y si la suma de las torcas se anula se conserva el momentum angular del sistema $\sum _i{l}_i$, a dicha suma también se le representa con el símbolo $L$$$\sum _i{\stackrel{⟶}{\tau }}_i=\frac{dL}{dt}\mathrm{.}$$ 

En general, por la Tercera Ley de Newton el conjunto de las torcas internas de los sistemas de partículas se anulan, por lo que sólo hace falta sumar las torcas externas al sistema.

Consideremos un objeto, o sistema de partículas, que esté rotando alrededor del eje $z$ y fijémonos en la iésima partícula, como muestra la figura 21 .

 

Figura 21: La iésima partícula de un sistema que rota en torno al eje $z$.

El momentum angular total del sistema se puede escribir de la siguiente manera

$$L=\sum _i{l}_i=\sum _i{m}_i\left(r_i\times v_i\right),$$pero si las partículas del sistema rotan todas con la misma velocidad angular $\stackrel{⟶}{\omega }$ el momento angular de cualquier partícula, incluida la iésima, es$$l_i=m_i{r}_i\times \left(\stackrel{⟶}{\omega }\times r_i\right)=m_i\left[\stackrel{⟶}{\omega }{r}_i^2-r_i\left(r_i\cdot \stackrel{⟶}{\omega }\right)\right]\mathrm{.}$$Si descomponemos el segundo término en sus componentes cartesianas lo anterior queda$$l_i=m_i\left[\stackrel{⟶}{\omega }{r}_i^2-\left(x_i\hat{i}+y_i\hat{j}+z_i\hat{k}\right)\left(r_i\cdot \stackrel{⟶}{\omega }\right)\right]$$y dado que la velocidad angular está en la dirección $z$, podemos sumar el primer término con el cuarto$$l_i=m_i\left\{\left[\omega r_i^2-z_i\left(r_i\cdot \stackrel{⟶}{\omega }\right)\right]\hat{k}-\left(x_i\hat{i}+y_i\hat{j}\right)\left(r_i\cdot \stackrel{⟶}{\omega }\right)\right\}\mathrm{.}$$Llevando a cabo el producto escalar implicado nos deja$$l_i=m_i\left\{\left[\omega r_i^2-z_i{r}_i\omega cos\theta \right]\hat{k}-\left(x_i\hat{i}+y_i\hat{j}\right)\left(r_i\omega cos\theta \right)\right\},$$pero $z_i=r_{i}cos\theta$, entonces$$l_i=m_i\left\{\left[\omega r_i^2-r_i^2\omega {cos}^2\theta \right]\hat{k}-\left(x_i\hat{i}+y_i\hat{j}\right)\left(r_i\omega cos\theta \right)\right\}\mathrm{.}$$Aquí tenemos que $\omega r_i^2-r_i^2\omega {cos}^2\theta =\omega r_i^2{sin}^2\theta$, por lo que$$l_i=m_i\left[\omega r_i^2{sin}^2\theta \hat{k}-\left(x_i\hat{i}+y_i\hat{j}\right)\left(r_i\omega cos\theta \right)\right]\mathrm{.}$$El radio de giro no es más que $R=r_{i}sin\theta$, lo que permite simplificar lo anterior $$l_i=\omega m_i{R}_i^2\hat{k}-\left(x_i\hat{i}+y_i\hat{j}\right)\left(m_i{r}_i\omega cos\theta \right)$$y ésto revela a la inercia rotacional de la partícula, $I_i=m_i{R}_i^2$, en la expresión$$l_i=I_i\stackrel{⟶}{\omega }-\left(x_i\hat{i}+y_i\hat{j}\right)\left(m_i{r}_i\omega cos\theta \right)\mathrm{.}$$El primer término tiene una forma sencilla $I_i\stackrel{⟶}{\omega }$, sin embargo, la otra parte del resultado tiene dirección radial y no es tan simple. Si el objeto que rota tiene otra partícula idéntica justo del otro lado del eje de rotación, al sumar esos dos momentos angulares se anula el térmono radial$$l_i+l_j=2I_i\stackrel{⟶}{\omega },$$más aún, si todo el objeto tiene simetría radial, el momentum angular $L$ del objeto se puede escribir de forma muy simple$$L=I\stackrel{⟶}{\omega }\mathrm{.}$$Como sabemos que $\sum _i{\stackrel{⟶}{\tau }}_i=\frac{dL}{dt}$, podemos concluir que si no hay torca neta sobre el objeto, el producto de la inercia rotacional por la velocidad angular se mantiene constante.

 

 Figura 22: Un patinador artístico varía su inercia rotacional para, a su vez, variar su rapidez angular. La poca fuerza de fricción con el hielo hace que el momento angular se conserve por un tiempo significativo. La animación original se puede ver en https://yzurus.tumblr.com/post/165891863870/donovan-carrillo-hasta-que-te-conoc%C3%AD-fs.

4.13 Ejemplos de conservación del momentum angular

4.13.1 Plataforma giratoria

Una persona está sentada sobre una plataforma giratoria sin fricción, que gira con una velocidad angular de ${\omega }_i=$1.22 rev/s. Los brazos de la persona están en cruz y en cada mano sostiene una pesa. Con sus manos en esta posición la inercia de rotación total de la persona, junto con las pesas y la plataforma, es de $I_i=$ 6.13 kg m${}^2$. Si al mover las pesas la persona disminuye la inercia de rotación a $I_f=$ 1.97 kg m${}^2$, (a) ¿cuál es la velocidad angular resultante de la plataforma? y (b) ¿cuál es la razón entre la nueva energía cinética y la energía cinética original?

Figura 23: Plataforma giratoria sin fricción. Figura inspirada en la que aparece en el undécimo capítulo de “Física para ciencias e ingeniería”, de Raymond A. Serway y John W. Jewett, editorial Cengage Learning, séptima edición.

(a) El momentum se conserva si la torca externa se anula, de modo que $$L_i=L_f,$$así que se debe cumplir$$I_i{\omega }_i=I_f{\omega }_f$$y se puede despejar ${\omega }_f$$${\omega }_f=\frac{I_i}{I_f}{\omega }_i=3.80 rev/s\mathrm{.}$$

(b) La razón de las energías cinética es $$\frac{E_{kf}}{E_{ki}}=\frac{\frac{1}{2}{I}_f{\omega }_f^2}{\frac{1}{2}{I}_i{\omega }_i^2}=\frac{I_f{\left(\frac{I_i}{I_f}{\omega }_i\right)}^2}{I_i{\omega }_i^2}=\frac{I_i}{I_f}=3.11$$La energía cinética aumenta poco más de tres veces. La persona debe hacer trabajo para disminuir la inercia rotacional, aquí no hay conservación de la energía.

 

$$\mathrm{ }$$